Vektorlar
Vektorning ta’rifi
Vektor deb kattalik va yo‘nalishga ega bo‘lgan qiymatga aytamiz. Masalan, \(\mathbf{a}(3, 4)\) vektor ikki o‘lchovli fazoda quyidagicha tasvirlanadi. Agar vektorning boshlang‘ich kordinatasi berilmagan bo‘lsa, u holda uni biz \((0, 0)\) deb olamiz, hamda har doim vektorlarni kichik lotin harflari bilan belgilaymiz va ularni qalin holda yozamiz. Lekin oddiy sonlarni ham kichik lotin harflari bilan belgilaymiz, faqat ular qalin bo‘lmaydi.
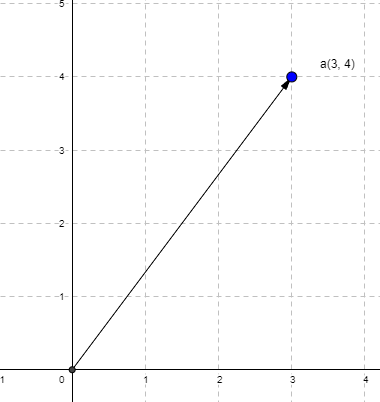
Biz ushbu darslar davomida uning geometrik xususiyatini hozircha qaramasdan, uning o‘rniga oddiy o‘zgaruvchi deb Python dasturlash tilida o‘rganamiz. Agar vektordagi qiymatlar soni boshqacha bo‘lsa, masalan \(\mathbf{a}(3, 5, 2, 6)\) unda bu kabi vektorlarni biz tasavur qilishimizning imkoni yo‘q. Shuning uchun ularning chizmasiga e’tibor bermasdan, uning o‘lchovi va yo‘nalishiga e’tibor beramiz. Hamda vektorni tashkil etuvchi qiymatlarni (so‘ngi holda, 3, 5, 2, 6) uning elementlari deb nomlaymiz. Agar uning biror elementiga murojaat qilmoqchi bo‘lsak, unda quyidagicha yozamiz \(\mathbf{a}_1\) va bu murojaatni indekslash deb ataymiz. Bu kab indekslash matematikaga xos bo‘lib, dasturlash tillarida bu narsa farqlanadi. Masalan, bizga elementlari haqiqiy sonlardan iborat bo‘lgan \(\mathbf{a}\) vektor berilgan desak, uni odatda quyidagicha ko‘rishida yozamiz: \(\mathbf{a}\in \mathbb{R}^n\). Demak \(\mathbf{a}\) vektorda \(n\) ta element bor va uning \(i\)-elementi \(\mathbf{a}_i\) bilan belgilanadi.
Eslatma. Biz vektorlarni belgilashda unlarning haqiqiy ko‘rinishdan foydalanmadik, aslida har bir vektor qiymatga va songa ega bo‘lgani uchun va ularni vektorligini anglatish uchun yo‘nalishini ham ko‘rsatishimiz kerak. Lekin bu yo‘nalishni matnlarda berishning iloji yo‘q, uning o‘rniga odatda biz \(\overrightarrow{\mathbf{a}}\) dan foydalanamiz, masalan yuqoridagi vektorni to‘g‘iri ko‘rinishi \(\overrightarrow{\mathbf{a}}(3, 5, 2, 6)\) bo‘ladi. Biz ushbu qo‘llanmada bu belgini ishlatmaymiz.
Eslatma. Bu yerda \(\mathbb{R}\) harfi har doim haqiqiy sonlar to‘plamini anglatadi. Misol uchun agar bizda \(b \in \mathbb{R}\) bo‘lsa, u holda biz \(b\) ning qiymati haqiqiy son deb tushunamiz hamda odatda biz bu son (o‘zgaruvchi) haqiqiy yoki butun deb yozmasdan shu qisqa belgilashdan foydalanamiz. Ushbu bosqichma-boshqich sohaga kirish, umid qilamizki kelajakda chuquroq fani o‘rganishga ko‘mak beradi.
Vektorlarni Pythonda tasvirlash
Ushbu turdagi o‘zgaruvchilarni e’lon qilish uchun Pythonda ikki xil o‘zgaruvchi turi mavjud ulardan birinchisi tuple(qulaylik uchun biz shu turdan foydalanib turamiz). Ushbu turda o‘zgaruvchi e’lon qilish uchun biz quyidagi qoidadan foydalanamiz: <o‘zgaruvchi nomi> = (<qiymatlar ro‘yxati>) - birinchi biz nomlamoqchi bo‘lgan o‘zgaruvchi nomini yozamiz, keyin esa tenglik belgisini qo‘yib, oxirida vektorning qiymatlarni qavs ichiga vergul bilan ajratib yozamiz. Misollar:
Eslatma. Ushbu Chiziqli algebra qismida biz Pythonning faqat tuple turni o‘rganib ketamiz, lekin ular haqida to‘liq Python dasturlash tilining ikkinchi qismida so‘z yuritamiz.
[ ]:
# a vektor o‘zgaruvchisi e'loni va uning qiymati
a = (3, 4)
# Chop qilish
print(a)
# 4 o‘lchovli vektor
b = (4, 6, 23, 6)
print(b)
# Agar bir o‘lchovchli bo‘lsa, har doim bitta vergul quyish shart, shunda oddiy sondan farq qiladi.
c = (4, )
print(c)
(3, 4)
(4, 6, 23, 6)
(4,)
Indekslash
Keling hozir biror insoni uning yoshi, bo‘yi va vazni bilan ifodalovchi vektorni qaraylik. Hammda shu misol orqali qanday qilib inkeslash Pythonda ishlashini tushunib olaylik. Matematikadan farqli ravishda, Pythonda indekslash har doim 0 dan boshlanadi, ya’ni \(\mathbf{a}_1\) ni ifodalash biz Pythonda a[0] deb kod yozamiz.
[ ]:
# inson: yoshi, bo‘yi va vazni
human = (18, 175, 70)
# uning har bir parameterni chop qilish
# agar insonning faqat yoshini chop qilmoqchi bo‘lsak,
# unda, uning 0 chi indeksini chop qilaylik
print(human[0])
18
E’tibor bering, biz hech qachon insoni ifodalovchi bir nechta qiymatlarni bitta o‘zgaruvchi ositga jamlaganimizda, har bir qiymatga o‘zgaruvchi e’lon qilmaymiz va human[0] deb uning yoshini tushunamiz, human[1] deb esa uning bo‘yining uzunligini. Agar indekslashda xato qilsak, masalan, qiymatlarning joyini almashtirib qo‘ysak, unda dastur bizga qiymatlarni chiqarishda davom ettaveradi, faqat natijalar xato bo‘ladi. Buni ko‘rish uchun keling, print funksiyasida nimani chop qilayotgan
ekanimizni matnlar orqali tasvirlaylik.
[ ]:
# inson: yoshi, bo‘yi va vazni
human = (18, 175, 70)
# yoshini chop qilish
print('Berilgan insoning yoshi:', human[0])
# agar indekslashda boshqa qiymat berib qo‘ysak
# unda ham ishlayveradi
print('Berilgan insoning yoshi:', human[2])
print('Berilgan insoning yoshi:', human[1])
Berilgan insoning yoshi: 18
Berilgan insoning yoshi: 70
Berilgan insoning yoshi: 175
Yuqoridagi kod bizga yaqqol ushbu turdagi xatolikni ko‘rsatib berdi. Shuning uchun biz har doim qaysi o‘ringa qanday qiymat qo‘yganimizni esalab qolishimiz hamda shunga mos ravishda ularga murojaat qilishimiz zarur bo‘ladi. Ushbu kodning oxirgi ikkitasi yosh qiymatini emas balki boshqa narsalarni chop qilmoqda. Biroq uning birinchisidagi qiymat 70 bunda yosh mavjud xato bo‘lsa ham, lekin ikkinchisi bizga aniq xatoligi ko‘rinib turibdi. Birinchi kabi xatolik bizga koddagi kamchiliklarni topishimizga xalaqit qiladi. Shuning uchun eng yaxshisi kodni yozishda e’tiborli bo‘lishdir. Quyidagi kod yuqoqirdagi kodning to‘liq va to‘g‘iri holatini ifodalaydi.
[ ]:
# inson: yoshi, bo‘yi va vazni
human = (18, 175, 70)
# yoshini chop qilish
print('Berilgan insoning yoshi:', human[0], 'yosh')
print('Berilgan insoning bo\'yi:', human[1], 'sm')
print('Berilgan insoning vazni:', human[2], 'kg')
Berilgan insoning yoshi: 18 yosh
Berilgan insoning bo'yi: 175 sm
Berilgan insoning vazni: 70 kg
Odatda biz qiymatlarning birligini xotirada saqlamaymiz, ularni mantiqan o‘zimiz bilamiz, lekin foydalanuvchiga (dasturdan kimdir foydalansa), unda biz ularga qiymatlar haqida qo‘shimcha axborotni berishimiz zarur bo‘ladi. E’tibor bering, biz quyidagicha matndan foydalandik 'Berilgan insoning bo\'yi:', ya’ni \ belgisi. Agar matnda tirnoq ‘ belgisini ishlatish zarur bo‘lsa, unda biz uning oldiga \ belgisini qo‘yishimiz yoki uni qo‘shtirnoq (”) belgisi yordamida yozishimiz kerak
bo‘ladi. Quyidagicha.
[ ]:
# inson: yoshi, bo‘yi va vazni
human = (18, 175, 70)
# yoshini chop qilish
print('Berilgan insoning yoshi:', human[0], 'yosh')
# Yuqoridagi va paski satrlar faqat tirnoq (')
# bilan yozilgan
# o‘rtadi esi qo‘shtirnoq bilan
print("Berilgan insoning bo‘yi:", human[1], 'sm')
print('Berilgan insoning vazni:', human[2], 'kg')
Berilgan insoning yoshi: 18 yosh
Berilgan insoning bo'yi: 175 sm
Berilgan insoning vazni: 70 kg
Vektorlar ustida amallar
Chiziqli algebra kursida vektorlar ustida ko‘plab amallarni ko‘rib o‘rganish mumkin. Lekin biz ushbu kitobda bizga zarur bo‘lgan amallarni kerakli o‘rinlarda ketma-ket o‘ganib boramiz. Ushbu amallarni tushinish uchun odatda biz geometrik usuldan foydalanamiz, aks holda bu amallar ba’zida ma’noga ega bo‘ladi. Ya’ni biz ularning ba’zilarini hayotiy tushunchalar bilan anglashimiz mumkin, ko‘plarini esa yo‘q. Masalan, yuqoridagi misoldagi kabi ikki insoni 3 qiymat bilan ifodalaylik va ularni bir biriga qo‘shaylik. Nima hosil bo‘ladi? Bu narsa bizga tushunarsiz. Lekin boshqa hollarda tushunish mumkin, masalan, inson faqat oylik moashi va bolalari soni bilan ifodalansa, unda ikki insoning moashining yig‘indisi va birgalikda bolalarining soni deb tushunish mumkin. Keling umumiylikni yuqotmasdan, vektorlar ustida amallarni ko‘rib chiqaylik. Ikkita \(\mathbf{x} \in \mathbb{R}^{n}\) va \(\mathbf{y} \in \mathbb{R}^{m}\) vektorlar berilgan. Ko‘p ishlatadigan amallar:
Ikki vektorni qo‘shish va ayirish amallari mos indekslardagi qiymatlarining yig‘idisi va ayirmasi bilan yangi vektor hosil qilishdir. Umumiy ko‘rinishi \(\mathbf{c}=\mathbf{a}\pm \mathbf{b}\). Agar har bir elementi bo‘yicha yozmoqchi bo‘lsak, u holda \(\mathbf{c}_1=\mathbf{a}_1+\mathbf{b}_1, \mathbf{c}_2=\mathbf{a}_2+\mathbf{b}_2,\mathbf{c}_3=\mathbf{a}_3+\mathbf{b}_3\). Pythonda kodi.
[ ]:
# ikkita butun turdagi tuple o‘zgaruvchisi
a = (2, 4, -3)
b = (4, 2, 5)
# ularning har bir elementini alohida alohida qo‘shish
# va yangi c vektorini hosil qilish
c = (a[0] + b[0], a[1] + b[1], a[2] + b[2])
# chop qilish
print('a+b=', c)
# ularning har bir elementini alohida alohida ayirish
# va yangi c vektorini hosil qilish
c = (a[0] - b[0], a[1] - b[1], a[2] - b[2])
# chop qilish
print('a-b=', c)
a+b= (6, 6, 2)
a-b= (-2, 2, -8)
Ushbu yig‘indining geometrik ma’nosi quyidagi ikki o‘lchovli koordinatalar sistemasida keltirilgan. Unga ko‘ra, agar ikki \(\mathbf{a}\) va \(\mathbf{b}\) vektorlarni bir-biriga qo‘shsak, u holda ikkisning yo‘nalishidan hosil bo‘lgan yangi vektorni tasavur qilamiz. Masalan, ikkita kishi aravani bir tomonga qaratib tortib ketyabdi va ularning tortish kuchlari orasida ma’lum bir burchak bor, shunda arava qandaydir tezlik bilan harakatlanishi mumkin.
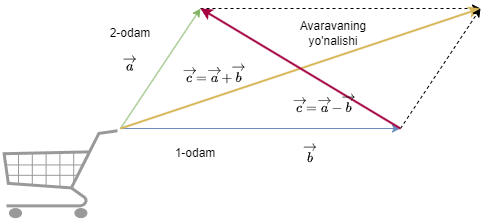
Ikki vektor o‘rtasida ko‘paytirish amalining bir nechta ko‘rinishlari mavjud:
Skalyar ko‘paytma (ko‘p adabiyotlarda nuqtali ko‘paytma (dot product)) deb, o‘lchami bir bolgan ikki vektorning mos elementlarining ko‘paytmasning yig‘indisi aytiladi. Hamda natija son bo‘ladi. Matematik ko‘rinishi, agar yuqoridagidek 3 ta elemenetdan tashkil topgan bo‘lsa, ya’ni \(\mathbf{a}, \mathbf{b} \in \mathbb{Z}^3\). \(c=\mathbf{ab}=\mathbf{a}_1\mathbf{b}_1+\mathbf{a}_2\mathbf{b}_2+\mathbf{a}_3\mathbf{b}_3\).
Tashqi ko‘paytma (outer product) ikki vektor elementlarning har bir elementlar hammasi bir biriga o‘zaro ko‘paytiriladi va natijada matritsa hosil bo‘ladi. \(\mathbf{x} \otimes \mathbf{y}\).
\[\begin{split}\mathbf{x} \otimes \mathbf{y} = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_m \end{pmatrix} \otimes \begin{pmatrix} y_1 & y_2 & \cdots & y_n \end{pmatrix} = \begin{pmatrix} x_1 y_1 & x_1 y_2 & \cdots & x_1 y_n \\ x_2 y_1 & x_2 y_2 & \cdots & x_2 y_n \\ \vdots & \vdots & \ddots & \vdots \\ x_m y_1 & x_m y_2 & \cdots & x_m y_n \end{pmatrix}\end{split}\]
[ ]:
# ikkita butun turdagi tuple o‘zgaruvchisi
a = (2, 4, -3)
b = (4, 2, 5)
# ularning har bir elementini alohida alohida qo‘shish
# va yangi c vektorini hosil qilish
c = a[0] * b[0] + a[1] * b[1] + a[2] * b[2]
# chop qilish
print('a*b=', c)
# tashqi ko‘paytma
C = ((a[0] * b[0], a[0] * b[1], a[0] * b[2]),
(a[1] * b[0], a[1] * b[1], a[1] * b[2]),
(a[2] * b[2], a[2] * b[1], a[2] * b[2]))
print("tashqi ko‘paytma: ", C)
a*b= 1
tashqi ko'paytma: ((8, 4, 10), (16, 8, 20), (-15, -6, -15))
Sonlar ustida mavjud bo‘lgan bo‘lish amali vektorlar ustida aniqlanmagan. Bunda biz bir vektorni ikkinchi vektorga “to‘liq” bo‘lshni nazarda tutamiz. Ya’ni ikki vektorni bo‘lish degan tushuncha yo‘q. Lekin, ba’zi amaliy masalarda biz vektorlarni elementlari bo‘yicha bo‘lishimiz mumkin va natijada esa yana vektor hosil bo‘ladi. Umumiy ko‘rinishi \(\mathbf{c}=\mathbf{a} / \mathbf{b}\). Agar har bir elementi bo‘yicha yozmoqchi bo‘lsak, u holda \(\mathbf{c}_1=\mathbf{a}_1/\mathbf{b}_1, \mathbf{c}_2=\mathbf{a}_2/\mathbf{b}_2,\mathbf{c}_3=\mathbf{a}_3/\mathbf{b}_3\). Pythonda kodi.
[ ]:
# ikkita butun turdagi tuple o‘zgaruvchisi
a = (2, 4, -3)
b = (4, 2, 5)
# ularning har bir elementini alohida alohida bo‘lish
# va yangi c vektorini hosil qilish
c = (a[0] + b[0], a[1] + b[1], a[2] + b[2])
# chop qilish
print('a/b=', c)
a/b= (6, 6, 2)
Vektorlarni transfanerlash amali har bir vektorga alohida qo‘llaniladi. Ushbu amal vektorni qator ko‘rinishdan ustun ko‘rinishga o‘tkazadi, lekin bunday amalni biz Pythonning
tupleturida farqlamaymiz. Matematika ko‘rinishi:\[\begin{split}\mathbf{y} = \begin{pmatrix} y_1 & y_2 & \dots & y_n \end{pmatrix} \quad \Rightarrow \quad \mathbf{y}^T = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix}\end{split}\]
Ikki vektor orasidagi masofa. Ushbu amalni sonlar ustida doimiy ishlatamiz hamda u har doim musbat bo‘ladi. Chunki biz ikki kishining yoshilarining farqi qancha desak unda biz, masalan, 15 yosh deymiz. Aslida esa kichigidan kattasini ayirsak unda manifiy son hosil bo‘ladi, aytaylik 45 yoshli odam 60 yoshli odamdning yoshidan ayirsak, unda -15 bo‘ladi. Bu esa ikkis orasidagi masofani, ya’ni farqni ifodalamaydi. Shuning uchun masofa musbat bo‘lishi kerak. Buning uchun biz matematikada sonning moduli degan tushunchani ishlatamiz, masalan, \(\vert \mathbf{a} \vert\). Bunda \(\mathbf{a}\) ning qiymati musbat bo‘lsa ham manifiy bo‘lsa ham musbat son chiqadi. Biz yuqorida fazoda tartib aniqlanmaganligi haqida bahs yuritgan edik, ya’ni bir vektorni ikkinchi vektordan katta yoki kichik deyish mumkin emas. Shuning uchun ham ikki vektor orasidagi masofa ma’lum bir shartlarni qanoatlantirishi kerak hamda eng asosiysi vektorlar nechta elementdan tashkil topishidan qattiy nazar masofa bitta son bo‘lishi kerak. Shundagina biz ularni solishtira olamiz. Ushbu amalni ikki vektorni parameter sifatida oluvchi funksiya ko‘rnishida yozamiz, ya’ni \(\rho(\mathbf{x}, \mathbf{y})\).
\(\rho(\mathbf{x}, \mathbf{y}) \geq 0\) - manifiy bo‘lmasligi zarur;
\(\rho(\mathbf{x}, \mathbf{y})=0 \leftrightarrow \mathbf{x}=\mathbf{y}\) - ikki vektorning hamma elementlari mos ravishda teng bo‘lsa, ularning orasidagi masofa 0 ga teng bo‘lishi kerak;
\(\rho(\mathbf{x}, \mathbf{y}) < \rho(\mathbf{x}, \mathbf{y}) + \rho(\mathbf{x}, \mathbf{z})\) - 3 ta vektor o‘rtalaridagi masofaning burchak sharti. Bu fazodagi 3 nuqtadan to‘g‘iri chiziqlar o‘tkazilganda uchburchak qoidasiga tushadi, shu sababdan ushbu xossa bo‘lishi kerak.
Biz ushbu masofalarga juda ko‘p misollar keltirishimiz mumkin, eng sodasi bu Evklid masofasi hisoblanib, u fazoda ikki nuqta orasidagi masofaga teng bo‘ladi va Pifagor teoremasi orqali aniqlanadi. Tassavur qilamiz bizda ikkita vektor bor, ya’ni, \(\mathbf{x}, \mathbf{y} \in \mathbb{R}^n\). Ular orasidagi Evkilid masofasi quyidagicha:
\begin{equation} \rho(\mathbf{x}, \mathbf{y}) = \sqrt{(\mathbf{x}_1-\mathbf{y}_1)^2+(\mathbf{x}_2-\mathbf{y}_2)^2+\dots+(\mathbf{x}_n-\mathbf{y}_n)^2} \end{equation}
Bunday masofani o‘lchovchi funskiyalar bilan kelajakda batafsilroq tanishamiz.
Vekrotning katta va kichik qiymatlarini hamda katta va kichik qiymatlar turgan o‘rini topish ham alohida amallar sifatida qaralsa bo‘ladi, lekin biz Python darslarimizda takrorlash amallarini o‘tmadik, shuning uchun bu yerda matematik ko‘rinishda berib ketamiz. Vektorning katta qiymatini odatda biz \(max(\mathbf{a})\) va kichik qiymatini esa \(min(\mathbf{a})\) ko‘rinishdagi funksiyalar bilan belgilaymiz. Masalan, \(\mathbf{a}=\{5, -3, 6, 7, 1\}\) bo‘lsa, u holda \(max(\mathbf{a})=7\) va \(min(\mathbf{a})=-3\). Xuddi shunday katta qiymat turgan o‘rini \(argmax(\mathbf{a})\) va kichik turgan o‘rini esa \(argmin(\mathbf{a})\) kabi funksiyalar bilan ifodalasak, unda yuqoridagi vektor natijalari \(argmax(\mathbf{a})=4\) va \(argmax(\mathbf{a})=2\) bo‘ladi.
Tartiblash amallarini ham vektorlar ustida kiritish zarur, chunki ko‘p o‘rinlarda biz ushbu amaldan keng foydalanamiz. Lekin Pythonda hozircha ushbu kodlarni yozmaymiz. Ushbu amalni ham funksiya ko‘rinishida quyidagicha kiritamiz: \(sort(\mathbf{a})\). Agar \(\mathbf{a}=\{4, -3, 6, 12, 1\}\) bo‘lsa, u holda \(sort(\mathbf{a})=\{-3, 1, 4, 6, 12\}\) bo‘ladi. Ushbu amal uchun ham obyektlarning o‘rni orqali tartiblash mumkin, u holda \(argsort(\mathbf{a})=\{2, 5, 1, 3, 4\}\) bo‘ladi.