Miqyoslash

Berilganlarni miqyoslash deganda biz ularning qiymatlarini yoki taqsimotini bir oraliqdan yoki taqsimotdan boshqa oraliqqa yoki taqsimotga ko‘chirishni tushinamiz. Masalan, biror mahsulotning vaznlari kilogrammlarda berilgan bo‘lsa, ularni grammlarga o‘tkazish yoki ushbu qiymatlarni boshqa biror oraliqqa ko‘chirishimiz zarur bo‘ladi. Chunki MO algoritmlari bularsiz yaxshi natijaga erishmaydi.

Normallashtirish

Ingliz tilidagi Normalization so‘zni biz Normallashtirish deb tarjima qildik. Ushbu so‘zga yaqin so‘zni oldingi qismda vektorlar ustida amal sifatida kiritdik. Lekin, bu yerda biz ozroq boshqacharoq tushuncha haqida so‘z yuritmoqchimiz, ammo, buni ham umumiy holda vektorlar ustida amalga oshirildi deyish mumkin. Keling birinchi muammoni qo‘yaylikda, keyin ushbu muammoni tushinib uni yechishga kirishaylik. Faraz qilaylik, \(\mathbf{x}\) va \(\mathbf{y}\) ikkita vektor berilgan bo‘lsin, hamda shu vektorlarning o‘rtasidagi Evklid masofasini o‘lchaylik. Ushbu vektorlarning har biri 3 tadan elementga ega bo‘lib, ya’ni \(\mathbf{x}, \mathbf{y} \in \mathbb{R}^3\), ular ikki odamning bo‘yining uzunligini metrlarda, yoshini yillarda va vaznini esa kilogrammlarda saqlasin. Masalan, \(\mathbf{x}=\{1.8, 25, 88\}\), \(\mathbf{y}=\{1.6, 78, 67\}\), ya’ni jadvalda ko‘radigan bo‘lsak:

#	Uzunligi	Yoshi	Vazni
1-odam, x	1.8	25	88
2-odam, y	1.6	78	67

Shu yerda eng e’tibor qiladigan holat - biz hech qachon vektorga yoki matritsaga har bir qiymat qanday o‘lchov birligida(masalan, kilogramm, metr, yil) bo‘lishini saqlamaymiz, uning o‘rniga shunchaki shunday deb tushunamiz va qayerda zarur bo‘lsa, shunday joylarda oshkor ravishda foydalanuvchi uchun yozib qo‘yamiz. Endi keling, shu ikki vektor o‘rtasidagi Evklid masofasini topsak: \(d(\mathbf{x}, \mathbf{y})=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+(x_3-y_3)^2}\), \(d(\mathbf{x}, \mathbf{y})=\sqrt{(1.8-1.6)^2+(78-25)^2+(88-67)^2}\), \(d(\mathbf{x}, \mathbf{y})=\sqrt{(0.2)^2+(53)^2+(21)^2}\), \(d(\mathbf{x}, \mathbf{y})=\sqrt{(0.2)^2+(53)^2+(21)^2} \approx 57\). Demak boshlang‘ich masofa taxminan 57 ga teng ekan. Navbatda, shu vektorlarni insoning bo‘yisiz tasvirlaylik, ya’ni \(\mathbf{x}=\{25, 88\}\), \(\mathbf{y}=\{78, 67\}\) va masofani qayta hisoblaylik. Bu holatda masofa yana shu taxminan 57 ga teng bo‘ladi. Bu esa bizga hozirgi holatda inson bo‘yining umuman ushbu masofaga ta’siri yo‘qligini anglatadi yoki ta’siri juda kichik bo‘lib, uni e’tiborga olish shart emas. Keyingi o‘rinda esa, ushbu muamoni yechish uchun inson bo‘yini metrlarda emas balki santimetrlarda o‘lchaylik, unda vektorlarimiz quyidagi ko‘rinishga ega bo‘ladi: \(\mathbf{x}=\{180, 25, 88\}\), \(\mathbf{y}=\{160, 78, 67\}\). Bu holda esa masofa taxminan 60 ga teng bo‘ladi. Hozir bizda savol tug‘ildi qaysi masofani olishimiz kerak, 57 yoki 60? Yoki biz quyidagi xulosaga kelishimiz mumkinmi Evklid masofasi yoki shu kabi masofalar turli qiymatlar chiqaradimi (unday emas)! Bu kabi savollar yoki muammolar yana topiladi. Shuning uchun ham masofani topishda avval qiymatlarni biror me’yorga, ya’ni normaga keltirish zarur bo‘ladi aks holda algoritm yaxshi tanlangan bo‘lsada, natija yomonligicha qoladi.

Normallashtirishning bir qancha usullari mavjud hamda ular bir biridan ma’lum bir kichik farqlarga ega. Agar, eslasangiz, biz statistika bo‘limida o‘zgaruvchi degan tushunchani kiritgan edik. Endi, bu yerda normallashtirishni bitta o‘zgaruvchining o‘zida qolganlariga bog‘lamasdan amalga oshirishimiz zarur bo‘ladi. Yodga solish uchun, bu yerda o‘zgaruvchi deb yoshni, vazni va uzunlikni alohida qaraymiz. Birinchi, eng sodda usul sifatida biz o‘zgaruvchini o‘zining joiz eng katta qiymatiga bo‘lish orqali amalga oshiramiz. Biz yuqoridagi namuna uchun inson yoshining taxminan chegarasini bilamiz, masalan, 120 yosh eng katta yosh bo‘lishi mumkin. Xuddi shunday, eng uzun odam 2.3 metr va eng og‘ir odam 200 kg deylik. Shunda yuroqidagi ikkita vektorning normallashgan ko‘rinishini quyidagicha hisoblaymiz: \(\mathbf{x}=\{\frac{1.8}{2.3}, \frac{25}{120}, \frac{88}{200} \}=\{ 0.78, 0.21, 0.44\}\) va \(\mathbf{y}=\{\frac{1.6}{2.3}, \frac{78}{120}, \frac{67}{200}\}=\{0.7, 0.65, 0.34\}\). Bu yerda har bir o‘zgaruvchini o‘zing mos eng katta qiymatiga bo‘lish orqali, biz har bir o‘zgaruvchining qiymatini 0 va 1 oralig‘ida qayta tasvirlaymiz. Shundagina, har bir o‘zgaruvchining masofaga ta’siri bir xil bo‘ladi. Aks holda yuqoridagi turli xillik bizda paydo bo‘ladi.

Ta’rif. Normallashtirish deb har bir o‘zgaruvchini ma’lum bir oraliqqa o‘tkazishga aytiladi.

Yuqoridagi namunada esa biz qiymatlarni \([0, 1]\) intervalga o‘tkazdik. Bu umumiy ta’rif esa bizga qiymatlarni ixtiyoriy oraliqa o‘tkazish imkonini beradi. Lekin, odatda Normallashtirishni \([0, 1]\) yoki \([-1, 1]\) oraliqqa o‘tkazish ma’qul hisoblanadi, ayniqsa MOda. Chunki, agar biz bir nechta o‘zgaruvchilar bilan biror natija olmoqchi bo‘lsak, u holda bu oraliqlar bizga eng yaxshi turg‘unlikni beradi.

Eslatma. Normallashtirish jarayoni odatda har bir MO modelini ishlab chiqishda bo‘ladi hamda uni biz berilganlarga dastlabki ishlov berish deymiz, bu atama Ingliz tilida esa data preprocessing deb nomlanadi.

Eslatma. Odatda, biror matematik modelga kiruvchi qiymatlar juda kichik miqdorda o‘zgardanda, masalaning natijasi o‘zgarmasa yoki juda kichik(arzimas darajada) o‘zgarsa, bu modelni turg‘un deb ataymiz. Yuqorida esa biz turg‘unlik deb shunga o‘xshash narsani aytik, lekin yuqoridagi turg‘unlik ko‘proq kiruvchi qiymatlarning qanday holatda ekanligiga bog‘liq hisoblanadi.

Biz yuqorida eng katta qiymatni tabiyatan mavjud tushunchalar orqali hosil qildik, ammo, bu narsani hamma o‘zgaruvchilar uchun qo‘llay olmaymiz. Shuning uchun ham, odatda, bunday eng katta qiymatlarni berilganlarning o‘zidan topish qulayroq, chunki turli mutaxasislar turlicha og‘irlik chegarasida faoliyat yuritishi mumkin. Masalan, bolalar shifokoriga 20 kg ham yetarli bo‘lishi mumkin, ya’ni eng og‘ir bola 20 kg bo‘lishi mumkin. Yuqorida biz faqat 2 ta obyekt(vektor, odam) oldik, shuning uchun ham, har bir o‘zgaruvchi uchun eng katta qiymat quyidagicha bo‘ladi: 1.8 metr uzunlik uchun, 78 yil yosh uchun va 88 kg esa vazn uchun bo‘ladi. Buni hisoblash ko‘rib turganimizdek juda sodda, ya’ni har bir o‘zgaruvchining qiymatlarining eng kattasini olish yetarlidir.

Eslatma. Biz yuqorida ikkita vektordagi mavjud qiymatlarni, masalan inson yoshlarini olib, uni statistikaga oid atama bilan o‘zgaruvchi deb yozdik, bu narsa MOda shunchaki alomat deyiladi. Ushbu atama boshqa sohalarda ham turlicha nomlanadi, masalan, tibiyotda ko‘rsatgich deb ham nomlanishi mumkin. Shuning uchun ham atamalardagi umumiylikni imkon qadar bilish zarur bo‘ladi, ya’ni biror manba o‘qiganimizda atama o‘zgarsa ham mazmunni tushunishimiz zarur bo‘ladi.

Keling endi, yuqoridagi o‘rgangan usulga asosan biror alamotni normallashtiraylik. Buning uchun birinchi biz alomat sifatida biror \(\mathbf{x}\) vektorni qaraylik, unda ushbu vektorning normallashgan ko‘rinishini quyidagicha ifodalash mumkin: \(\mathbf{x}^{*}=\frac{\mathbf{x}}{max(\mathbf{x})}\), bu yerda \(max()\) funksiyasi berilgan vektorning eng katta qiymatini topadi. Siz o‘quvchiga bir narsa adashtiradigan tuyilishi mumkin, ya’ni yuqorida biz vektor deb bir insoning 3 ta ko‘rsatgichini(vazni, yoshi, bo‘yining uzunligini) olgan edik. Lekin yuqoridagi oxirgi \(\mathbf{x}\) vektor bu bitta odamning bir nechta ko‘rsatgichlari emas, balki berilgan hamma odamning bitta ko‘rsatgichini o‘zida saqlaydi. Masalan, 100 ta odamning yoshini. Agar shu odamlarning yoshi eng kattasi 70 yoshda bo‘lsa, hamma odamning yoshini shu songa bo‘lib chiqamiz.

Hozirgacha o‘rgangan normallashtirish usuli odatda maksimal normallashtirish deyiladi hamda ushbu usul qiymatlarni har doim ham \([0, 1]\) oraliqqa o‘tkazmaydi, balki \((0, 1]\) o‘tkazadi. Shuning uchun ham ko‘pincha biz quyidagi normallashtirish usulidan foydalanamiz: \(\mathbf{x}^{*}=\frac{\mathbf{x} - min(\mathbf{x})}{max(\mathbf{x})-min(\mathbf{x})}\), bu yerda \(max()\) va \(min()\) funksiyalari berilgan vektorning eng katta va eng kichik qiymatlarini qaytaradi. Agar \(\mathbf{x}\) vektorning eng kichik qiymati nolga teng bo‘lsa, u holda oldingi usul bilan bu usul bir xil bo‘ladi, ya’ni \([0, 1]\) oraliqqa o‘tkazadi.

Eslatma. Agar biz oraliqni belgilashda \([a, b]\) ko‘rinishdagi qavslardan foydalansak, u holda oraliqning ikki tomonidagi qiymatlar ham kiradi deb hisoblaymiz va buni odatda to‘liq oraliq yoki interval deb ataymiz. Agar shuni o‘zgartirsak, ya’ni \((a, b]\) ushbu holda oraliq \(a\) sonidan boshlanib \(b\) sonida tugaydi, lekin \(a\) soni hisoblanmaydi va \(b\) soni oraliqqa kiradi. Masalan, biror son \((10, 100]\) oraliqda deyilsa, u holda bu son \(11, 12, \dots, 100\) bo‘lishi mumkin. Bunday oraliqlarni biz yarim-ochiq oraliq deb ataymiz. Agar \((a, b)\) bo‘lsa, u holda buni ochiq oraliq deymiz.

Ushbu qismda biz ikki xil normallashtirish usullari bilan tanishdik. Hozir esa umumiy nazariy qism va atamalar bilan tanishib ularni mulohaza qilamiz. Birinchidan, statistika sohasida va MOda umumiy ikkita tushuncha bor: normallashtirish (buni me’yorlashtirish deb tarjima qilish mumkin) va standartlashtirish (Ingliz tilida standardization, O‘zbek tilida balki qoliplash deyish mumkindir). Normallashtirish deb biror qiymatni qat’iy belgilangan oraliqqa o‘tkazish tushinilsa, standartlashtirish deb esa, biz o‘zgaruvchining o‘rtacha qiymatini nolga va farqlanishini esa birga teng qilishga aytamiz. Ikkinchidan, mashinaga hech qachon o‘lchov birliklarini yozmaymiz hamda mashina uni qabul qilmaydi. Uning o‘rniga esa biz o‘zimiz bu haqida qayg‘uramiz, ya’ni har doim mashinga biror kiruvchi qiymatni berayotganimizda uni normallashtirib yoki standartlashtirib olamiz. Uchunchidan, agar bizning umumiy modelimizda shu kabi normallashtirish jarayoni mavjud bo‘lsa, u holda bu modelni o‘lchovga (yoki umumiy holda kiruvchi qiymatga) nisbatan o‘zgarmas deymiz. Ushbu o‘zgarmas atamasi Ingliz tilida invariant deb nomlanadi. Hamda bu normallashtirish orqali deyarli hamma modellar kiruvchi qiymatga nisbatan o‘zgarmas bo‘ladi, aks holda natijalar kutilganidek bo‘lmaydi. Nihoyat, quyida biz odam yoshi yillarda hamda uning uzunligi metrlarda berilgan holda, normallashtirish ikki o‘zgaruvchiga qanday ta’sir qilishini ko‘rishimiz mumkin. Buning uchun birinchi ushbu o‘zgaruvchilarni tasodifiy ravishda tanlab olamiz, hamda keyin ularning boshlang‘ich ko‘rinishi va normallashgan ko‘rinishini nuqtalar sifatida rasmda tasvirlaymiz qilamiz.

# kutubxonalar
import numpy as np
import matplotlib.pyplot as plt

# 200 yoshlarni va vaznlarni tasodifiy hosil qilamiz
# yosh [1, 120) intervalda
ages = np.random.randint(1, 120, size=200)
# vazn [1, 2.3] intervalda
weights = 1 + 1.3 * np.random.rand(200)

fig, axes = plt.subplots(2, 1)
fig.set_size_inches(10, 10)
# birinchi normallashmagan qiymatlarni
# nuqtalar sifatida chiqaramiz
axes[0].scatter(ages, weights)
axes[0].set_aspect('equal', adjustable='box')
axes[0].set_xlabel("Yosh")
axes[0].set_ylabel("Vazn")
axes[0].grid(True)
axes[0].set_title("Normallashga va normallashmagan qiymatlarning solishtirmasi")

ages = (ages - ages.min()) / (ages.max() - ages.min())
weights = (weights - weights.min()) / (weights.max() - weights.min())

axes[1].scatter(ages, weights)
axes[1].set_aspect('equal', adjustable='box')
axes[1].set_xlabel("Yosh")
axes[1].set_ylabel("Vazn")
axes[1].grid(True)

plt.show()

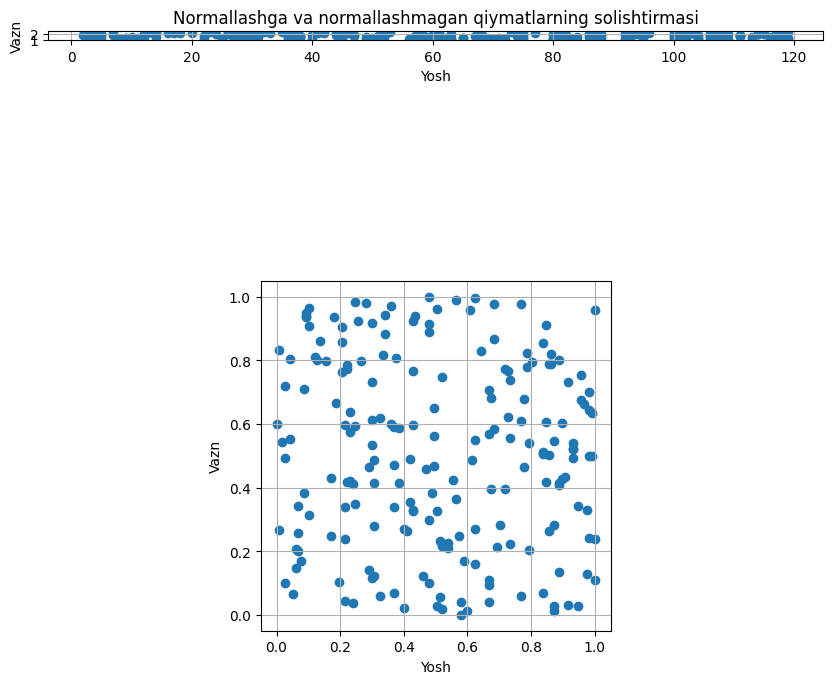
E’tibor bering, birinchi holda yoshning qiymati kattaligindan vazning ahamiyati deyarli qolmagan. Lekin normallashtirilgandan so‘ng esa, bu narsa pastki rasmda mavjud emas. Ushbu rasmlar bizga tasviriy jihatdan normallashtirishni qanday tushunishimiz kerakligini ko‘rsatadi.

Standartlash

Oldingi mavzuda sizlar bilan normallashtirish haqida so‘z yuritdik. Standartlashtirish normallashtirishning bir ko‘rinishi bo‘lib, asosan taqsimotning xususiyatlarini o‘zgartirishga hissa qo‘shadi. Biz haligacha taqsimotning umumiy ta’rifini rasmiy ravishda bermaganimiz uchun bu yerda shunchaki qanday qilib standartlashtirish mumkinligini eng ko‘p qo‘llaniladigan usullardan biri bo‘lgan, Z-baho(Ingliz tilida Z-score)ni qanday qo‘lashni sodda qilib keltiramiz: \(\mathbf{x}^{*}=\frac{\mathbf{x} - mean(\mathbf{x})}{std(\mathbf{x})}\), bu yerda \(mean()\) va \(std()\) funksiyasilari mos ravishda berilgan vektorning o‘rtacha va standart og‘ishini qaytaradi. Quyida esa yuqoridagi tasviriy dasturning natijalarini ushbu standartlashtirishda ko‘rishimiz mumkin:

ages = np.random.randint(1, 120, size=200)
weights = 1 + 1.3 * np.random.rand(200)

fig, axes = plt.subplots(2, 1)
fig.set_size_inches(10, 10)
# birinchi normallashmagan qiymatlarni
# nuqtalar sifatida chiqaramiz
axes[0].scatter(ages, weights)
axes[0].set_aspect('equal', adjustable='box')
axes[0].set_xlabel("Yosh")
axes[0].set_ylabel("Vazn")
axes[0].grid(True)
axes[0].set_title("Normallashga va normallashmagan qiymatlarning solishtirmasi")

ages = (ages - ages.mean()) / ages.std()
weights = (weights - weights.mean()) / weights.std()

axes[1].scatter(ages, weights)
axes[1].set_aspect('equal', adjustable='box')
axes[1].set_xlabel("Yosh")
axes[1].set_ylabel("Vazn")
axes[1].grid(True)

plt.show()

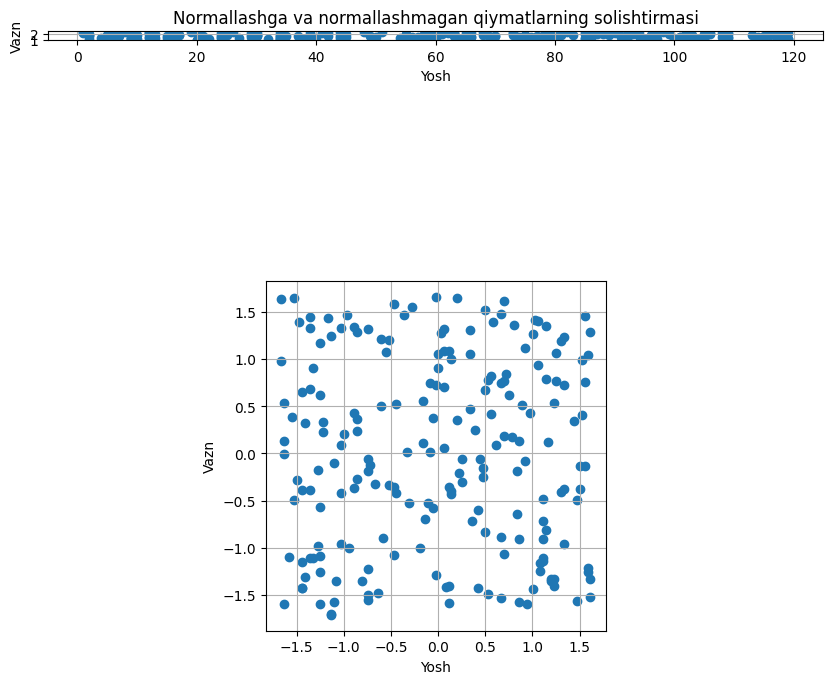
Normallashtirishda biz shunchaki qiymatlarini \([0, 1]\) intervalga ko‘chirgan bo‘lsak, bu yerda esa standartlashtirilgandan so‘ng qiymatlarning o‘rtachasi taxminan nolga teng bo‘lishi kerak hamda farqlanish esa birga. Ushbu ko‘rinishga keltirishdan asosiy maqsad, berilgan o‘zgaruvchini standart normal taqsimot sifatida tasvirlashdir. Ushbu taqsimotlar haqida keyingi statistika darslarimizda to‘liq ma’lumot beramiz.